Chapter 11 Class Notes

you are here > Class Notes - Chapter 11 - Lesson 11-2

Printable version

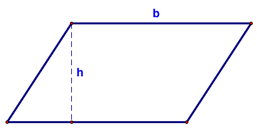
Area of Parallelograms and Triangles - Lesson 11-2

Today, we looked at how to find the area of a couple of different shapes. We started with a parallelogram:

Parallelogram Area Step 1

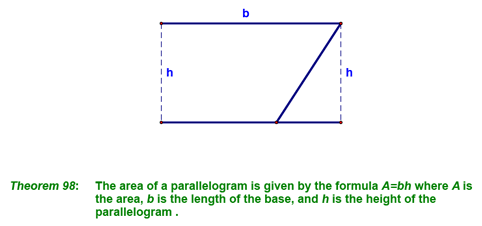
We noted that if we cut out the triangle on the left, we could move it to the other side and form something (a rectangle) for which we already have an area formula:

Parallelogram Area Step 2

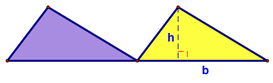
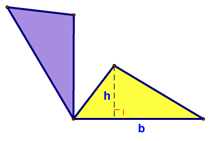
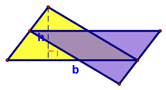
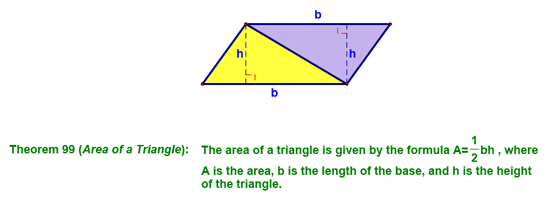
We then looked at how to find the area of a triangle. We started with a triangle (the yellow one), made a copy of it (the purple one) and translated it (to the left):

Triangle Area Derivation Step 1

Then rotated it clockwise:

$Triangle Area \Derivation Step 2$

Then translated it (up) again:

Triangle Area Derivation Step 3

Until we had a shape for which we already had an area formula (a parallelogram):

Triangle Derivation Step 4